|
These files are in dd_extra.tar.gz and include the following,
rule sample automatic classification files:
- for 1d, v=2, full lookup table,
as before but renamed,
- v2k5ss.sta (k=5)
- v2k6ss.sta (k=6)
- v2k6ss.sta (k=7)
- for 1d, multi_value, full lookup table,
- v3k3ss.sta (v=3 k=3)
- v4k2ss.sta (v=4 k=2)
- v4k3ss.sta (v=4 k=3)
- v5k2ss.sta (v=5 k=2)
- for 2d, multi-valye kcode,
- v3k4bs.sta (v=3 k=4)
- v3k5bs.sta (v=3 k=5)
- v3k6bs.sta (v=3 k=6)
- v3k7bs.sta (v=3 k=7)
- v4k4bs.sta (v=4 k=4)
- v4k6bs.sta (v=4 k=6)
glider/complex rule sample files for loaded on-the-fly with "g":
- for 1d, v=2, full lookup table,
as before but renamed,
- g_v2k5.r_s (k=5)
- g_v2k6.r_s (k=6)
- g_v2k7.r_s (k=7)
- for 1d, multi_value, full lookup table,
- g_v3k3.r_s (v=3 k=3)
- g_v3k4.r_s (v=3 k=4)
- g_v4k2.r_s (v=4 k=2)
- for 2d/3d, kcode lookup table,

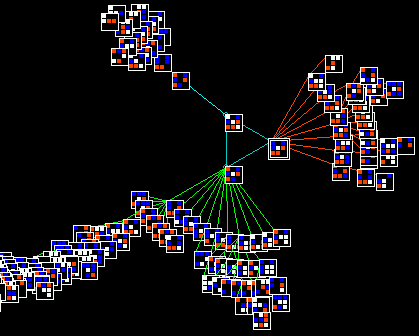
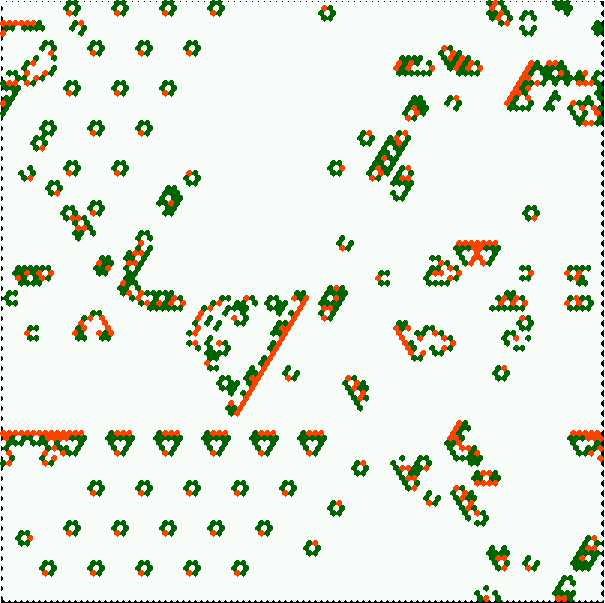
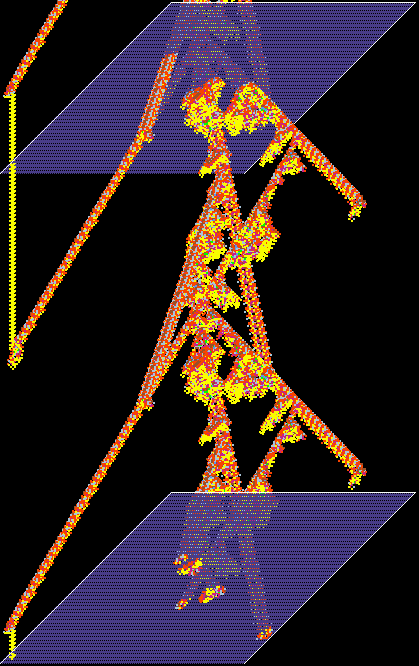
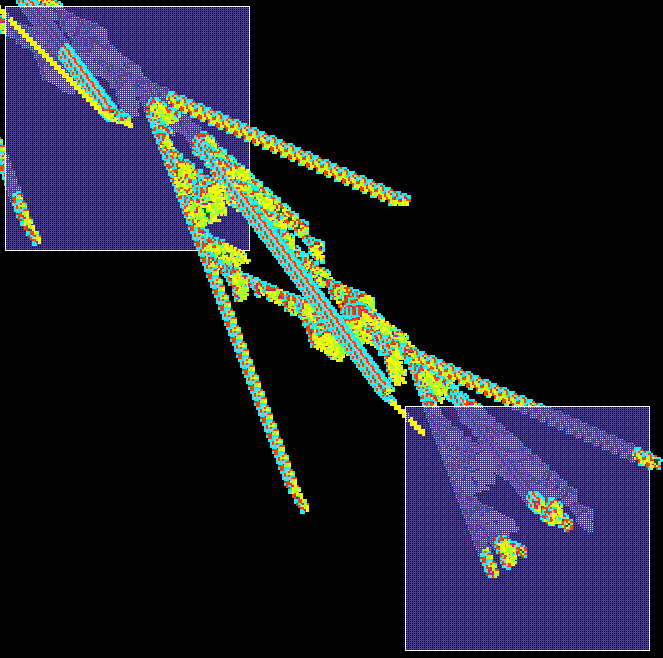
An automatically classified sample of about 16000 v=3 k=6 kcode rules
for 2d hex CA
Axies are as follows:
x=standard deviation of the input-entropy,
y=mean entropy, z=frequency of rules on the xy scatter plot.
Complex rules are spread out on the right with higher standard deviation,
Chaotic and ordered rules are on the left with
low standard deviation - chaos has high entropy (the tower),
and order lower entropy.
| |